Equations and Inequalities
Given a cubic equation $(x−1)(x−2)(x−3)>0$ as often seen in H2 Mathematics, you can solve this easily by sketching a graph.
Since when $x \rightarrow \infty $, y is +ve, start sketching the graph from the 1st quadrant. The turning points are at x = 1, x = 2 and x = 3. Since the factors are all linear terms (power 1), make a U-turn whenever it crosses the x-axis.
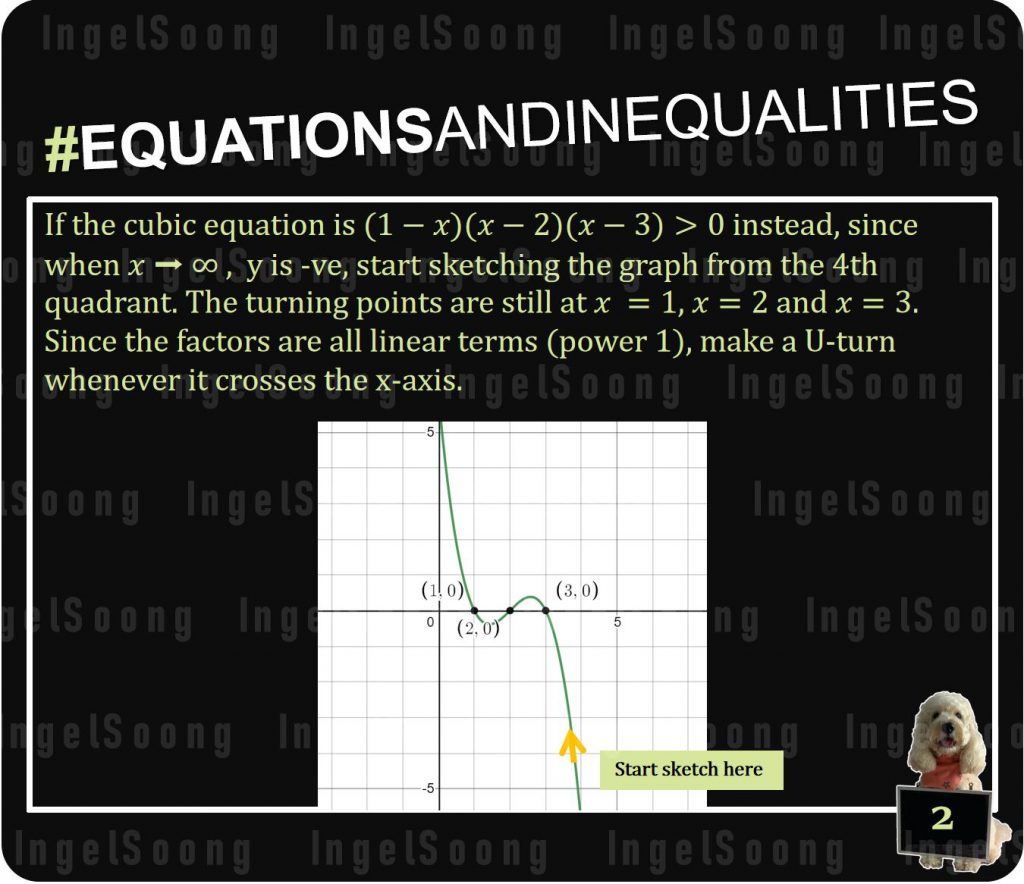
If the cubic equation is $(1−x)(x−2)(x−3)>0$ instead, since when $x \rightarrow \infty $ , y is -ve, start sketching the graph from the 4th quadrant. The turning points are still at x = 1, x = 2 and x = 3. Since the factors are all linear terms (power 1), make a U-turn whenever it crosses the x-axis.
If you have a quadratic equation $(x−1)^2(x−2)(x−3)>0 $, since when $x \rightarrow \infty $ , y is +ve, start sketching the graph from the 1st quadrant. The turning points are still at x = 1, x = 2 and x = 3. Forthe factors that are linear terms (power 1), make a U-turn whenever it crosses the x-axis. For the factor that is quadratic (power 2), make a U-turn without crossing the x-axis.