Oscillations Summary
Here’s an “ingelious” way on JC A Level H2 Physics Oscillations summary for Simple Harmonic Motion.
Let’s proceed to derive all the equations.
$x = x_0cos\omega t $
$cos\omega t = \frac{x}{x_0}$
$v = \frac{dx}{dt} = -x_0\omega^2sin\omega t $
$ = \mp x_0\omega \sqrt{1-cos^2\omega t} $
$ = \mp x_0\omega \sqrt{1-\frac{x^2}{x_o^2}} $
$ = \mp \omega\sqrt{x_0^2-x^2} $
$a = \frac{dv}{dt} = -x_0\omega^2cos\omega t $
$ = -\omega^2x_0 $
Total energy
$ KE = \frac{1}{2}mv^2 = \frac{1}{2}m\omega^2(x_0^2-x^2) $
$ TE = \frac{1}{2}mv^2 = \frac{1}{2}m\omega^2(x_0^2) $
$ PE = \frac{1}{2}mv^2 = \frac{1}{2}m\omega^2(x^2) $
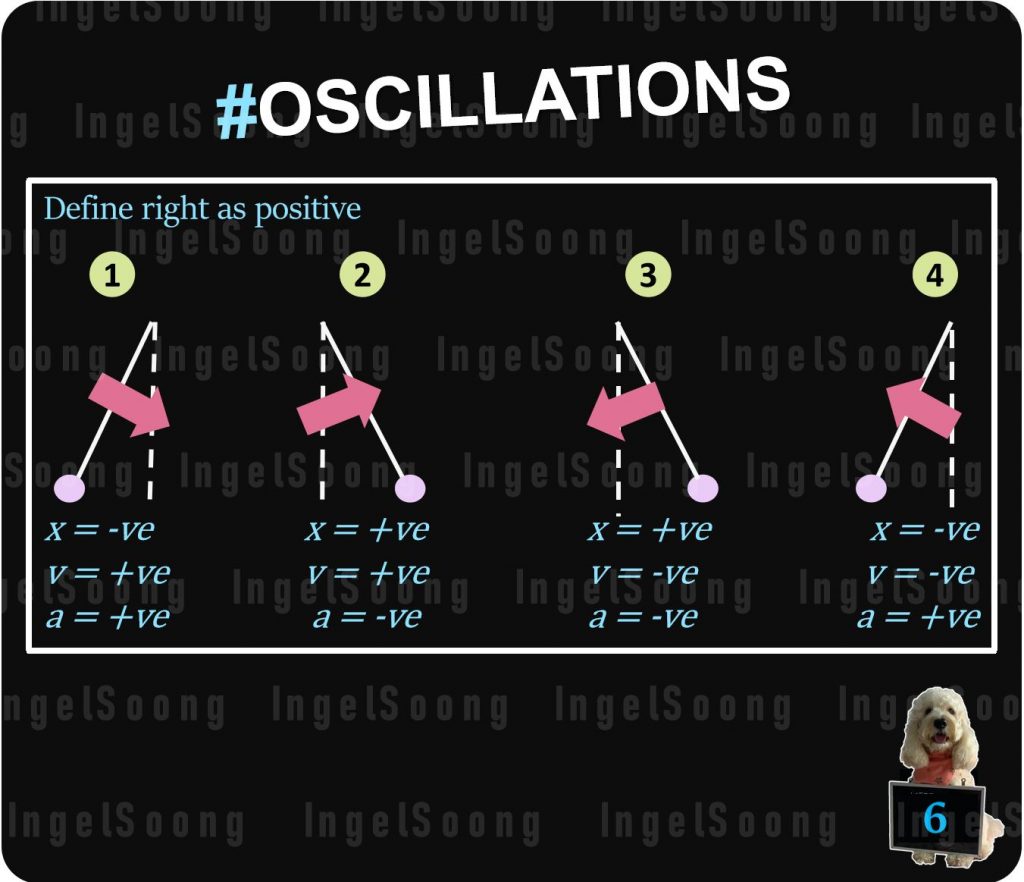
Define right as positive and track displacement x, velocity v and acceleration a as the pendulum completes a period.
The movement of the pendulum can be illustrated on a a-x graph as shown:

The movement of the pendulum can also be illustrated on a v-x graph as shown:

The total energy is always constant.
The kinetic energy is maximum at the amplitude, minimum at the equilibrium.
The potential energy is minimum at the amplitude, maximum at the equilibrium.







