Functions
Here’s an “ingelious” way on H2 Mathematics Functions summary.
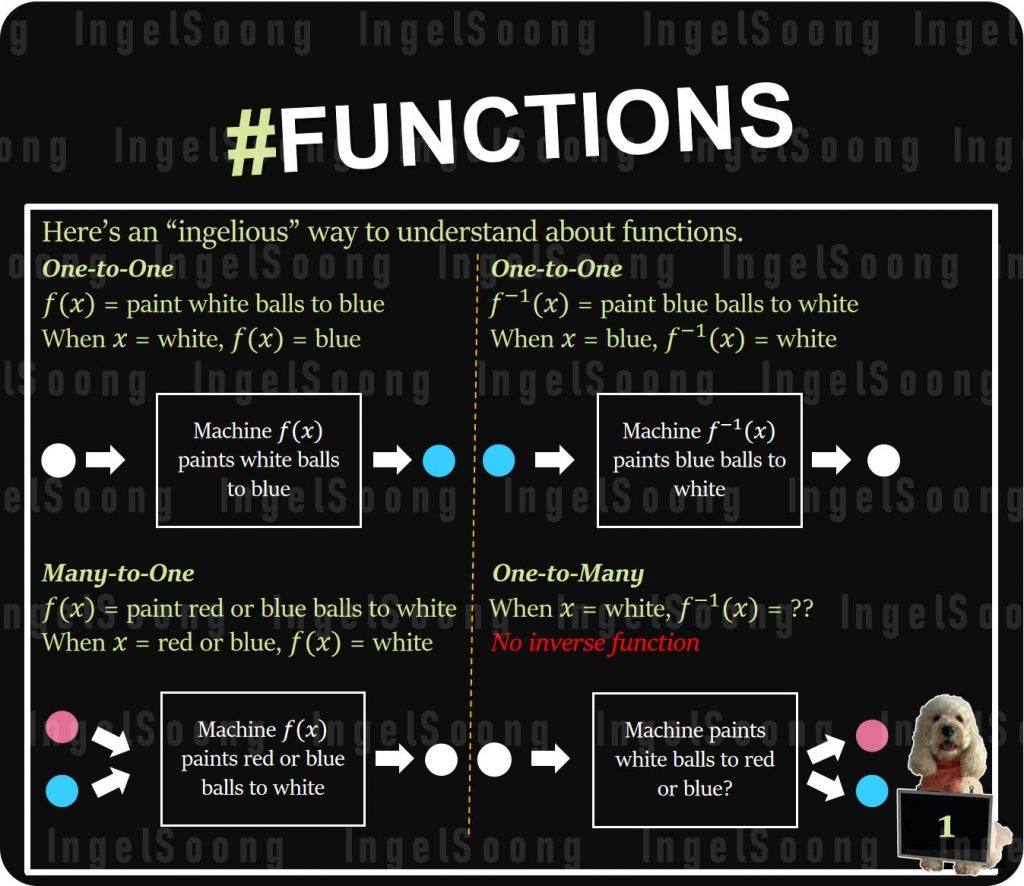
One-to-One
$f(x)$ = paint white balls to blue
When x = white, $f(x)$ = blue
One-to-One (inverse function)
$f^{-1}(x)$ = paint blue balls to white
When x = blue, $f^{-1}(x)$ = white
Many-to-One
$f(x)$ = paint red or blue balls to white
When x = red or blue, $f(x)$ = white
One-to-Many (no inverse function)
When x = white, $f^{-1}(x)$ = ??
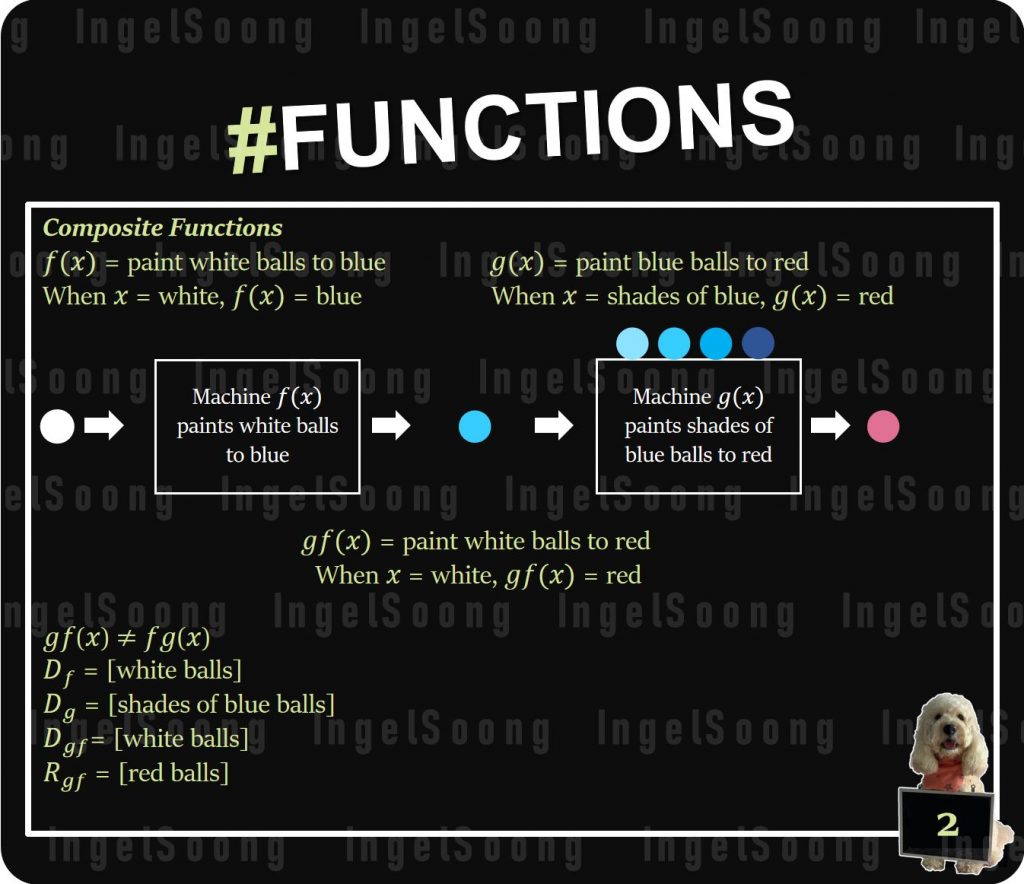
Composite Functions
$f(x)$ = paint white balls to blue
When x = white, $f(x)$ = blue
$g(x)$ = paint blue balls to red
When x = shades of blue, $g(x)$ = red
$gf(x)$ = paint white balls to red
When x = white, $gf(x)$ = red
$gf(x) \neq fg(x) $
$D_f$ = [white balls]
$D_g$ = [shades of blue balls]
$D_{gf}$= [white balls]
$R_{gf}$ = [red balls]
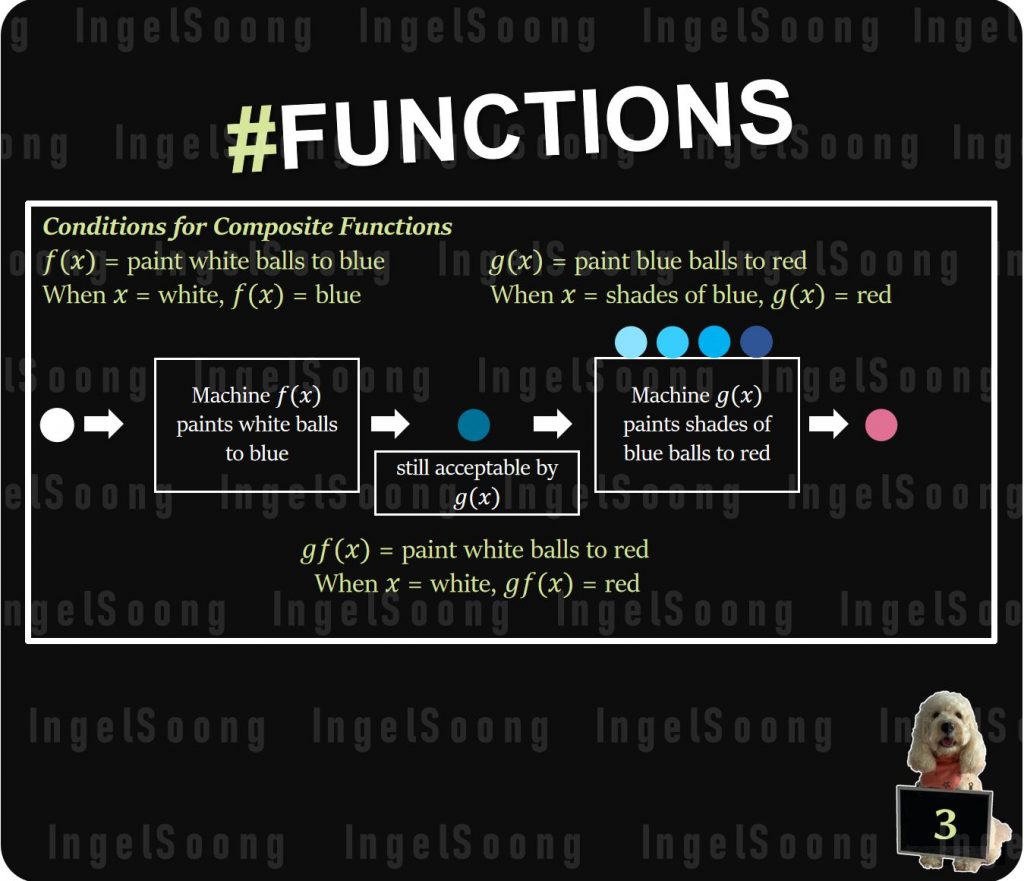
Conditions for Composite Functions
If $f(x)$ changes, such that
$f(x)$ = paint white balls to orange
When x = white, $f(x)$ = orange
$g(x)$ = paint blue balls to red
$gf(x)$ = paint white balls to red
When x = white, $gf(x)$ = undefined
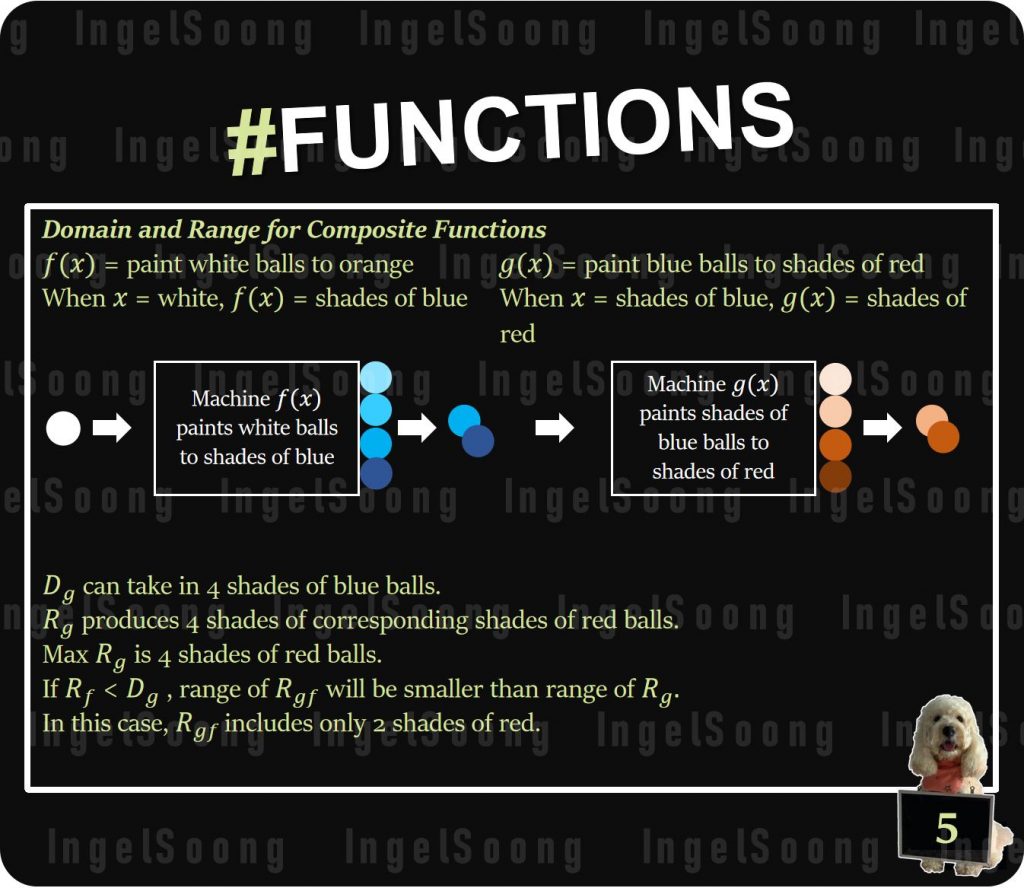
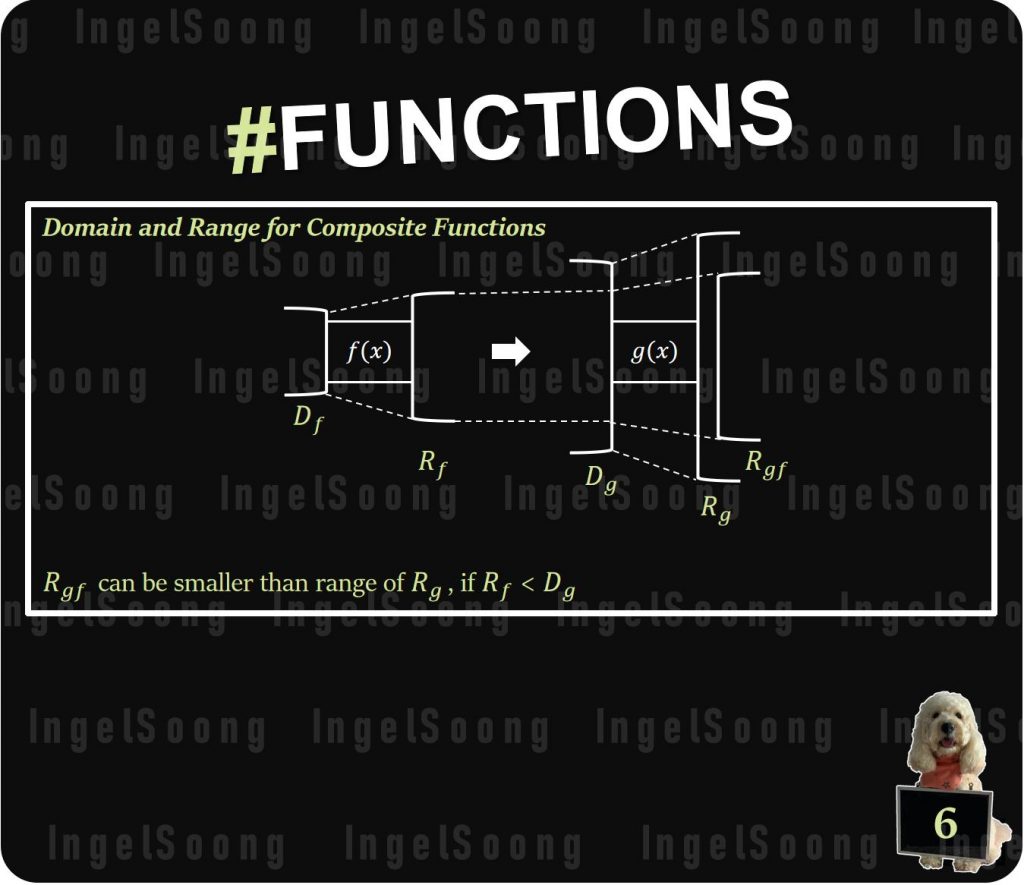
Domain and Range for Composite Functions
$f(x)$ = paint white balls to orange
When x = white, $f(x)$ = shades of blue
$g(x)$ = paint blue balls to shades of red
When x = shades of blue, $g(x)$ = shades of red
$D_g$ can take in 4 shades of blue balls.
$R_g$ produces 4 shades of corresponding shades of red balls.
Max $R_g$ is 4 shades of red balls.
If $R_f$ < $D_g$ , range of $R_{gf}$ will be smaller than range of $R_g$.
In this case, $R_{gf}$ includes only 2 shades of red.
$R_{gf}$ can be smaller than range of $R_g$ , if $R_f < D_g$